I recently taught a class on geometric series in which I gained interesting insights on the manner of problem solving exhibited by students when navigating a new topic. Moving forward, I accordingly plan to incorporate these learnings in my instructional and assessment related methodology.
In particular, I had supplemented my lecturing of introducing the topic with my personalized worksheet’s incomplete details, which initiated the inquiry from students on the different parameters involved in the geometric series formula. In reference to image A, the students were actively involved in assisting me to complete the details elucidating each part of the rule for finding geometric sum.

The first two problems shown in image A were observed to be solvable by most as they all the required parameters, namely, the first term (A1), common ratio (r) and number of terms (n) were all provided to straightforwardly implement them as inputs to evaluate the sum. However, the problems that followed (given in image B) after question 2, particularly questions such as number 3 and number 5 drew more confusion and consequently demanded my assistance by several students.
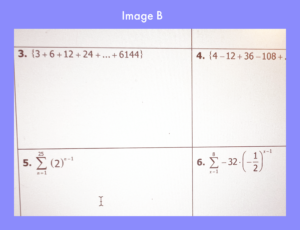
If we make a note of the distinction between problem 2 and problem 3, it would be apparent that what has changed is the given parameter of n. The latter does not explicitly provide the value of n, which has to be obtained from applying the knowledge of an earlier taught concept – the geometric sequence formula. This rule, shown in image C, is required to obtain the value of n (as the unknown “precursor” to finding the ultimate value of the sum of series).

After finding n from the sequence rule in image C ( the other parameters required are already obtainable from the question), one will proceed to use it for geometric sum formula in image A. At this juncture, I observed that many students could not recall the sequence formula or in general were puzzled by the missing n as the question was not presented with the straightforward accounting of knowns and unknowns that only use the geometric sum rule. A similar issue appeared for many students for question 5, in which the sequence and its terms are represented by the summation notation. It had to be clarified that the first and last terms have to be evaluated from this summation and that the index n is given by subtracting the first and last index. It was also tricky for many to identify that n is not always the “last” index on top of the summation sign in case the starting index is not 1).
All in all, this teaching session showed me that to reinforce a concept to students (of geometric sequences, in this case), one should provide an assortment of problems on the topic that ask ultimately the same value, yet, present themselves in more than one different form; as such, the case of finding the ultimate unknown will not appear as a one-step process. And, in this way, one would be forced to inquire and discern – where any and all parameters in the formula come from. My task here, as an instructor was not make it an exercise of merely “giving away” these insights; rather, I sincerely attempted to stir students’ inquiry and gently nudge them in the right direction of thinking process that approaches the solution.
